Premier interféromètre astronomique amateur
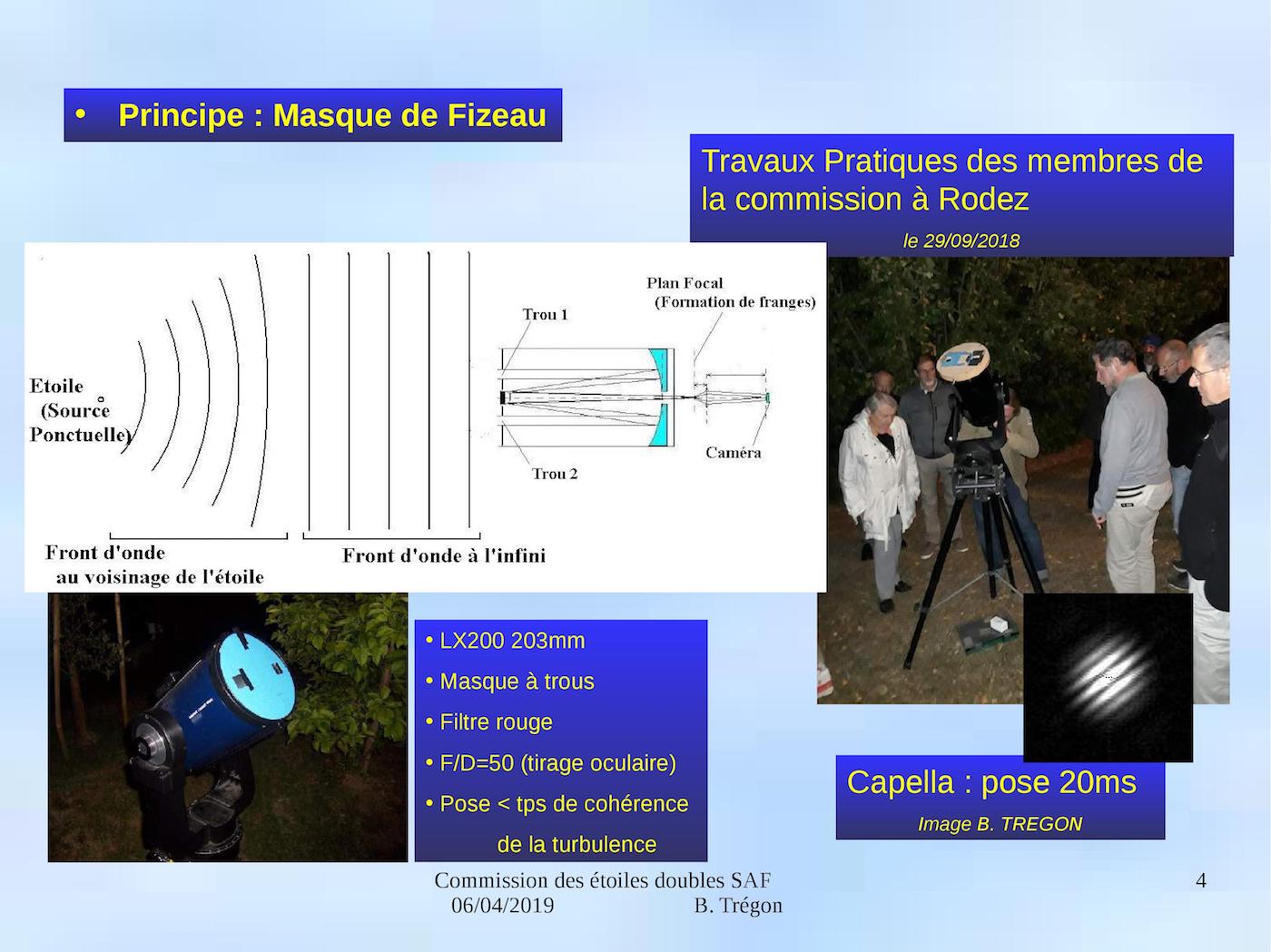
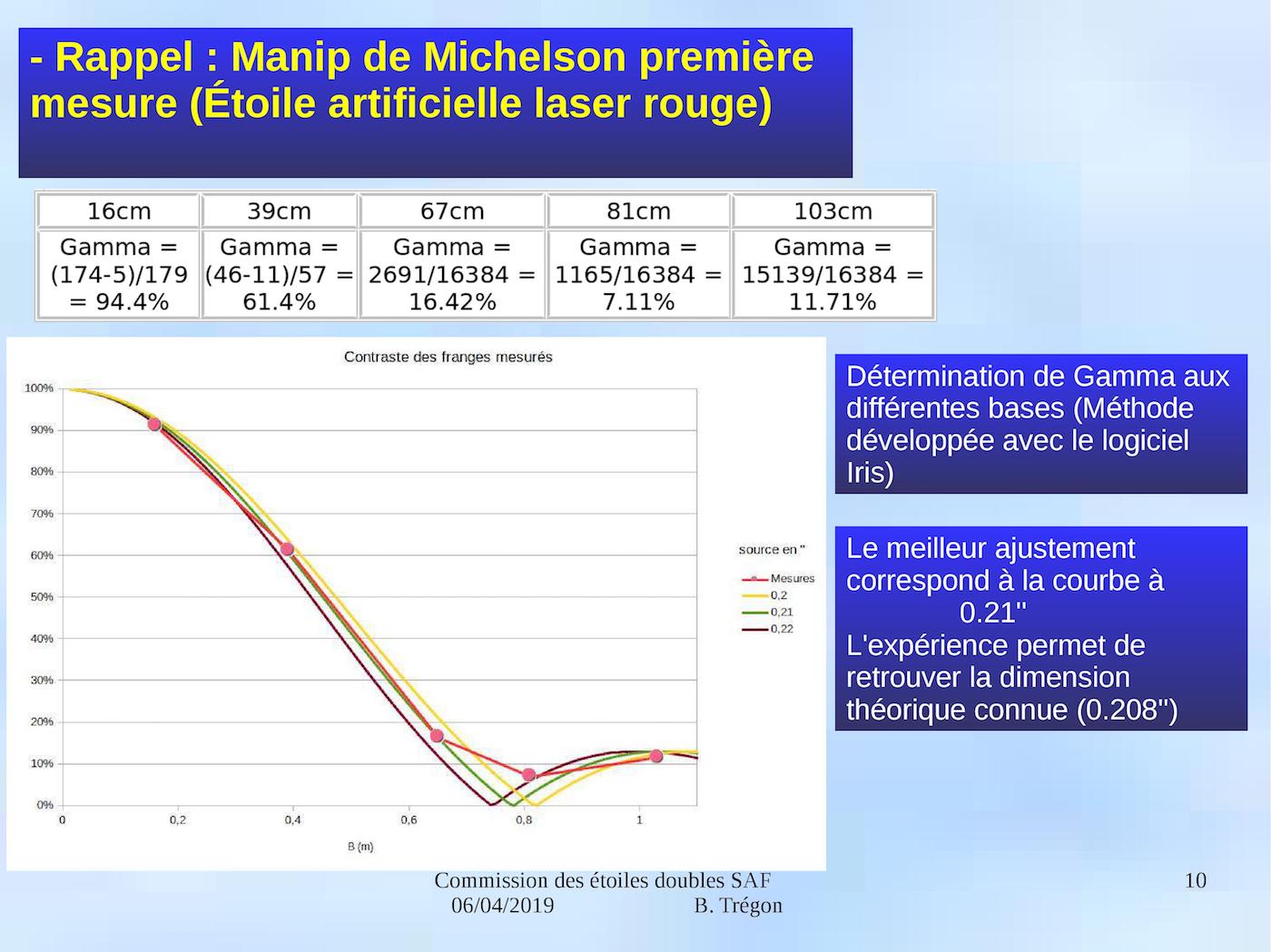
Bernard Trégon, membre de la commission des étoiles doubles de la SAF, a réussi à créer le premier interféromètre astronomique amateur pour l’observation des étoiles doubles. Il a présenté cette avancée remarquable lors de la Journée des commissions de la SAF, le 9 juin 2019 et nous explique brièvement ses travaux ci-dessous.
Bernard a un pied dans le monde professionnel et un pied dans le monde amateur : de profession, il est Ingénieur de Recherche au CNRS (Laboratoire Ondes et Matière d’Aquitaine UMR 5798) où il travaille dans le domaine de la physique en tant qu’électronicien et instrumentaliste pour des physiciens. Sa passion pour l’astronomie l’a amené à rencontrer Antoine Labeyrie dans un cadre professionnel et qu’il lui a proposé de participer activement au projet Hypertélescope, sous l’égide de l’Observatoire de la Côte d’Azur (OCA).